Generative A.I is A.I that creates entirely new data (images, videos, text) based on existing information. But being able to generate by itself is not inherently special. For instance, we can also generate data points from a normal distribution, what makes generative AI powerful? How does an A.I model learn what is “interesting” to generate?

Preliminaries

Generative Adversarial Networks, or GANs, is a framework for training such generative AI models (The other dominant framework being diffusion models).

Architecturally, it consists of two competing neural networks, a generator, and a discriminator. The generator network is the generative model that we are trying to train, while the discriminator scaffolds the generator, by discriminating between the real images and the A.I generated images.

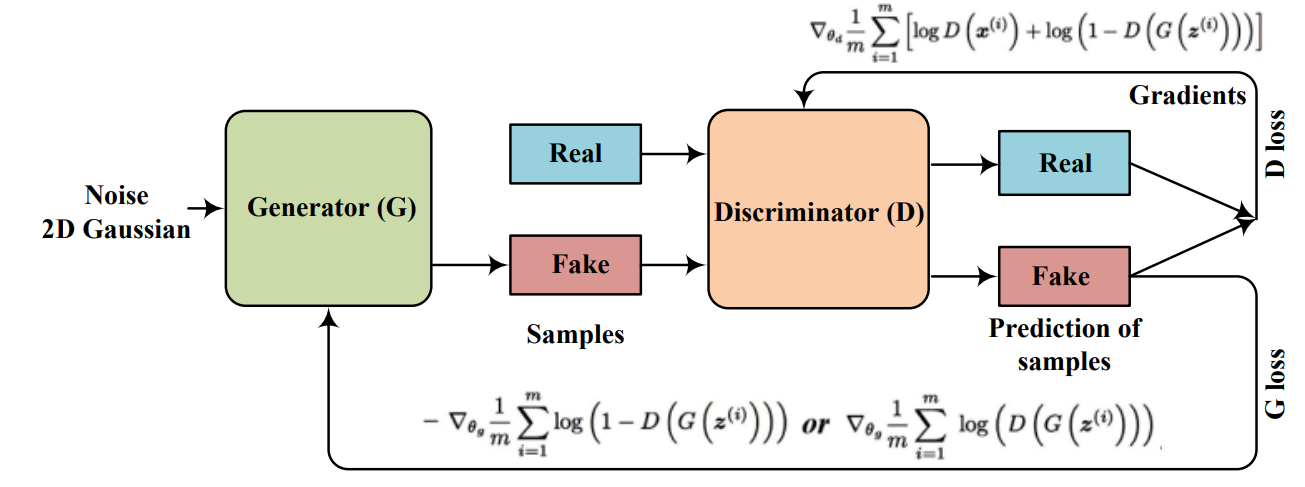
gan_architecture
Basic GAN Architecture [source]

How can we train the model?

Training means, updating the model parameters/weights. To do that, we need to define the objective function ir loss, and take steps towards minimising that objective function.


Deriving the objective function

Our goal is to derive $\mathcal{L}_{GAN}(G, D)$. There are three part to this:

(1) The Discriminator’s loss on real images and generated images
(2) The Generator’s loss on generated images

The calculation of all 3 of these losses, are dependent directly on the Binary Cross Entropy loss of the Discriminator. Recall the BCE-loss for a single instance is

\[\mathcal{L}_{BCE} = - (\mathbb{E}_y [y \times \log \hat{p}(y) + (1-y) \times \log \hat{p}(1-y)])\]

(1) The Discriminator’s loss on real images and generated images

For GAN-Discriminator, $y=1$ is a label on real images from the actual distribution, and $1-y$ is the label on fake images from the generated distribution.

For real image($x$) from the distribution of real images($P(x)$), and fake image ($x’$) generated by passing a random vector ($z \sim P(z)$) through a Generator ($G(z)$). The BCE-Discriminator loss is given by:

\[\mathcal{L}_{Discriminator} = - (\mathbb{E}_{x \sim P(x)}[\log D(x)] + \mathbb{E}_{x' \leftarrow G(z), z\sim P(z)} [\log (1 - D(x'))])\]


(2) The Generator’s loss on generated images

The Generator tries to “fool the discriminator” on generated images. I.e., it tries to maximise the BCE-loss of the discriminator, hence the loss which it tries to minimise, is the negative of the BCE-loss.

\[\mathcal{L}_{Generator} = - \mathcal{L}_{BCE-Discriminator} \\ \mathcal{L}_{Generator} = - (- \mathbb{E}_{x' \sim G(z), z\sim P(z)} [\log (1 - D(x'))]) \\ \mathcal{L}_{Generator} = \mathbb{E}_{x' \sim G(z), z\sim P(z)} [\log (1 - D(x'))]) \\\]

Note: The Generator only has gradients on the generated images, hence it’s loss and gradient is only going to be computed on the generated images.


Combining both objectives to get the minimax formulation

\[\begin{align} \mathcal{L}(G,D) &= \max_G \min_D \mathcal{L}_{Discriminator} \\\ &= \min_G \max_D - \mathcal{L}_{Discriminator} \end{align}\]

These two forms are actually equivalent, but the second form, $min_G max_D$ is the standard equation used. Possibly to highlight that the main target model is the Generator, hence it is framed in terms of minimising this loss.

\[\begin{align} \mathcal{L}(G, D) &= \min_G \max_D - \mathcal{L}_{Discriminator}\\ &= \min_G \max_D (\mathbb{E}_{x \sim P(x)}[\log D(x)] + \mathbb{E}_{x' \leftarrow G(z), z\sim P(z)} [\log (1 - D(x'))]) \end{align}\]

People might expect to see this form $\log 1 - D(G(z))$ instead of $(\log 1 - D(x’)$ in the equation, but I prefer the form I’m using here, as it conceptually shows $x$ versus $x’$ side by side.


Additional Notes

1.Implementation

The custom training class here follows the above logic of conceptually separating the model updating steps into (1) and (2), and basing all of the gradient updates off Pytorch BCELoss.

for epoch in range(self.num_epochs):
  for i, batch in enumerate(self.dataloader):
    fake_images = self._generate_fake_images(batch)
    lossD = self._train_discriminator(batch, fake_images)
    lossG = self._train_generator(batch, fake_images)
  ...

2.Implications of the minimax problem

Due to the form of the objective, GANs are a minimax problem rather than an optimisation problem. In typical optimisation problems, the goal is just to minimise or maximise an objective function. For the minimax problem, there are two competing objectives. Hence the goal is to reach a Nash equilibrium where neither players can improve their loss.


References

Pytorch DCGan Tutorial