Preliminaries

Bayes Risk

The Bayesian approach in decision theory, is an average-case analysis of an action $\alpha$, over all $\theta \in \Theta$ parameters of a distribution that specifies potential outcomes.

The ‘risk’ refers to the expected loss $\mathbb{E}[\mathcal{L}(\theta, \alpha)]$, where the expectation is taken over the probability distribution of $\theta$. The Bayes Risk for a single action, can be written as:

\[\mathrm{BR}(\alpha) = \mathbb{E}_{\theta\sim p(\theta)}[\mathcal{L}(\theta, \alpha)]\]

Minimum Bayes Risk

We typically want to choose an action amongst the space of all possible actions, that minimises the Bayes Risk. Intuitively this is kind of like saying, there is uncertainty in what the world will throw at me from $\theta \sim p(\theta)$, so we’re going to pick the action that will deal with it best on expectation.

\[\alpha^* = \mathrm{argmin}_{\alpha \in \mathcal{A}} \mathbb{E}_{\theta \sim p(\theta)} [\mathcal{L}(\theta, \alpha)]\]

When our action is choosing an estimator of $\theta$ that has minimum risk among all estimators, this is known as the Minimum Bayes Risk Estimator (or simply Bayes Estimator):

\[\theta^* = \mathrm{argmin}_{\hat{\theta}(x) \in \Theta(x)} \mathbb{E}_{\theta \sim p(\theta)} [\mathcal{L}(\theta, \hat{\theta}(x))]\]

MBR as a decision rule makes a lot of sense if we had a good handle on the distribution $p(\theta)$ and a meaningful loss function $\mathcal{L}$, for instance if the space of actions was what medical intervention to perform ($\alpha \in \mathcal{A})$, and we had some estimate of the probability of underlying condition of the patient, and a loss associated with each action and condition.


Minimum Bayes Risk Decoding

MBR Decoding is a particular flavor of finding the Bayes optimal action, where the action is a sequence (decoding). This method had been introduced in Automatic Speech Recognition[1] and Statistical Machine Translation[2]. Given a source input $x$ which can be speech signal or source language, the space of possible hypothesis $h \in \mathcal{H}(x)$, a probability distribution over decoded sequences $p(y|x)$, and a loss function $\mathcal{L}(y, h)$, the MBR decode for a source input $x$, is given by:

\[h^* = \mathrm{argmin}_{h \in \mathcal{H}(x)} \mathbb{E}_{p(y|x)} [\mathcal{L}(y, h)]\]

In theory, we would like to have a distribution over reference sequences $p(y|x)$ (for e.g, if we collected multiple human annotations). However at inference time, this is typically not available, and the model’s distribution $p_{\mathrm{model}}(y|x)$ is used as a proxy distribution for $p(y|x)$, as well as used to construct $\mathcal{H}(x)$.

MBR decoding is intractable (infinite hypothesis space) and most of it is research on the design choices of
(i) how to construct the space of hypothesis $\mathcal{H}(x)$,
(ii) how to construct the monte-carlo set of samples $y \in \mathcal{Y}$ to approximate $\mathbb{E}_{p(y|x)}$, and
(iii) the choice of loss function $\mathcal{L}$ which could be BLEU, METEOR or cheaper metrics like precision.
(iv) how to renormalise samples $y$ from $p(y|x)$ - with a small number of samples, the sequences are unlikely to be repeated and the monte-carlo estimate would give them all uniform probability.


Many papers[3,4,5] can be written just by varying these decision choices and studying the impact of them. As Ding Shuoyang pointed out at MT reading group, this can even be used to study problems with evaluation metrics when they are formulated as Loss functions.



MBR Decoding VS MAP Decoding (approximated by Beam Search)

MBR Decoding is an alternative to Beam Search, which is today’s default decoding heuristic for sequence models. Beam Search tries to find the Maximum Posterior decode by approximating the search space with a running list of candidate greedy-decodes.

\[\hat{y} = \mathrm{argmax}_y p(y|x; \theta_{\mathrm{MLE}})\]

The maximum posterior decode can be seen as a special case of MBR decode, when the loss function is the identity function. Then the only component that matters is the probability over sequences.


But MBR Decoding is not really minimising Bayes Risk, it’s just Consensus Decoding

Ultimately, MBR Decoding of this flavour reduces to consensus decoding from samples drawn from $p_{\mathrm{model}}(y|x)$ rather than finding the sequence that “minimises the Bayes Risk” of the distribution that we actually care about $p^*(y|x)$.

Both the hypothesis space $\mathcal{H}(x)$ and the monte carlo estimate of \(\mathbb{E}_{p(y|x)}\) uses samples drawn from $p_{\mathrm{model}}(y|x)$ — we can use top-p, beamsearch sampling, lookahead sampling, whatever decoding hackery method, but ultimately with a standard sentence similarity loss, the decision rule amounts to ‘find the sequence which is similar to everything else, on average’.


Why does it work and when does it not?

In the following sketch, we constructed a hypothesis space from sampling the sequences $y_1, y_2, y_3, y_4 \sim p(y|x)$, where $p(y|x)$ is the model’s distribution. For (a), $y_4$ is a pathological sequence, such as the empty string, or heavily repeated n-grams. If we had used MAP Decoding (or Beam Search), the most probable sequence would be $y_4$. However with MBR decoding (consensus decoding), lower probability sequences would be selected because of similarity to the other sampled sequences.

For (b), $y_4$ might be the most probable and “best” sequence, however due to consensus scoring against $y_1, y_2, y_3$, the MBR decoding decision rule might select $y_2$. In this scenario, the pathological sequence is not sampled at all as it has a low probability.

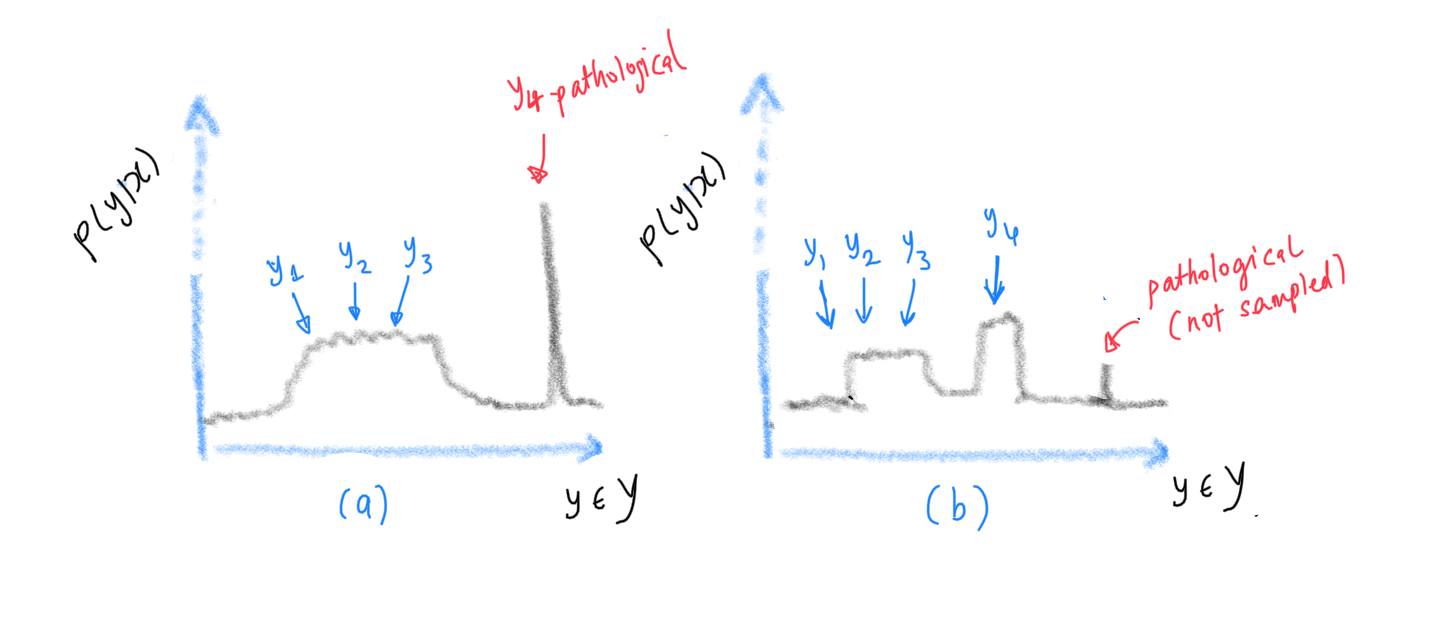image So, it depends on what the learned $p(y|x)$ looks like. But of course we don’t know beforehand, and it may require experimentation with decoding methods to actually find out.

Comments

  1. For dealing with pathological sequences, it seems like a principled albeit expensive $O(N\times S)$ where $N$ is the size of the hypothesis space and $S$ is the size of the set used to compute expectation. There could be much more practical ways to deal with pathological sequences.

  2. The flexibility of the expected risk equation allows us to pile on different loss functions on to the decoding stage. Why not just have $\mathcal{L}(y, \mathrm{minlength})$ for e.g? However the flavor of the original theory of MBR is already long lost and I hope anyone who tries to do this doesn’t call this MBR anymore.

  3. This post doesn’t mention anything about MBR training or MBR Decoding with lattices. That’s another story for another time.

References

[1] Vaibhava Goel and William J Byrne. 2000. Minimum bayes-risk automatic speech recognition. Comput. Speech Lang.
[2] Shankar Kumar and William Byrne. 2004. Minimum Bayes-risk decoding for statistical machine translation. NAACL.
[3] Bryan Eikema and Wilker Aziz. 2020 0. Is MAP decoding all you need? The inadequacy of the mode in neural machine translation. Coling.
[4] Mathias Müller and Rico Sennrich. 2021. Understanding the properties of minimum bayes risk decoding in neural machine translation. ACL.
[5] Bryan Eikema and Wilker Aziz. 2021. Sampling based minimum bayes risk decoding for neural machine translation.