Coordinate Ascent Mean-field Variational Inference (Univariate Gaussian Example)

Model Preliminaries

1. Variational Inference is used to approximate posterior densities for Bayesian models as an alternative strategy to MCMC.

2. Given a (joint) model, $p(X, Z)$, with latent variables $Z = z_1, … z_m$, and observations $X = x_1, .. x_n$. we are often interested in computing the posterior $p(Z|X)$, the probability of our latent variables given the data.

3. Often the exact posterior $p(Z|X)$ is intractable to calculate. Thus we aim to optimise a different distribution $q$, from a family of convenient distributions $Q$ over the latent variables, and minimize the KL divergence to the exact posterior.

\begin{equation} q^*(Z) = argmin_{q(z)\in Q} KL(q(Z) || p(Z|X) ) \end{equation}

1. The KL is not tractable either because it requires us to compute $p(X)$. Well the marginal log likelihood can be decomposed into the following, therefore maximising the ELBO is equivalent to minimising the KL divergence.

\begin{equation} log p(X) = ELBO(q) + KL(q(Z) || p(Z|X)) \end{equation}

Coordinate Ascent Variational Inference

• The mean field variational family describes a family of distributions where the latent variables are mutually independent and $q$ factorizes such that

\begin{equation} q(Z) = \prod_{j=1}^m q_j(z_j) \end{equation}

• A general expression for the optimal solution $log p (q_j^* (z_j))$ is given by: \begin{equation} log p(q_j^*(z_j)) \propto \mathbb{E}_{i\neq j}[log p(X, Z)] \end{equation}

• Because each $q_j^*(z_j)$ can be computed wrt to the other factors where $i\neq j$, each update is valid (since it doesn’t depend on itself). But requires cycling/iterating through the factors until convergence because of dependence on a factor that has been recently updated.

• Note when considering $q_j^* (z_j)$ we only need to consider terms that have some dependence on $z_j$ because other terms can be considered constants that do not affect $q_j^*$.

Pseudocode for CAVI

(from david Blei)

Joint distribution $p(X, Z)$
Variational density $q(Z) = \prod_{j=1}^{m}q_j(z_j)$
Variational Factors $q_j(z_j)$
$ELBO = \mathbb{E}[logp(Z, X)] - \mathbb{E}[logq(Z)]$

while ELBO has not converged
     for $j \in {1, …, m}$
         Set $log p (q_j(z_j)) \propto \mathbb{E}_{i\neq j}[log p(X, Z)]$
     end
     compute ELBO
end

Concrete Examples in Gory Detail

Univariate Gaussian

1. Specify the generative model:

1. The joint distribution is: \(\begin{align} p(X, Z) &= p(X, \mu, \sigma^2) \\\ &= p(X | \mu, \sigma^2) p(\mu | \sigma^2) p(\sigma^2) \end{align}\)

2. The variational density is: \(\begin{align} q(Z) &= \prod_{j=1}^m q_j(z_j) \\\ q(Z) &= q(\mu, \sigma^2) \\\ &= q_\mu(\mu) q_{\sigma^2}(\sigma^2) \\\ \end{align}\)

3. ELBO to check convergence. Note the dependence of $\mu$ on $\sigma^2$ under $p$ but their independence under $q$. \(\begin{align} ELBO(q) &= \mathbb{E}[logp(Z, X)] - \mathbb{E}[log q(Z)] \\\ &= \mathbb{E}[logp(X|Z) + logp(Z)] - \mathbb{E}[log q(Z)] \\\ &= \mathbb{E}[logp(X|\mu, \sigma^2) + log p(\mu|\sigma^2) + logp(\sigma^2)] - \mathbb{E}[log q(\mu) + logq(\sigma^2)] \end{align}\)

4. Optimal factor equation for iterative updates \begin{equation} log q_j(z_j) = \mathbb{E}_{i\neq j}[log p(X, Z)] + C \end{equation}

Expectation $\mathbb{E}$ is evaluated wrt $\sigma^2$, and all terms that do not depend on $\mu$ are collapsed into the constant $C$. \(\begin{align} log q^*(\mu) &= \mathbb{E} [ logp(X| \mu, \sigma^2) + logp(\mu | \sigma^2) + logp(\sigma^2)] + C \\\ &= \mathbb{E} [logp(X|\mu, \sigma^2) + logp(\mu| \sigma^2)] + C \end{align}\)

Recall pdf of a normal distribution: \(\begin{align} p(x_i|\mu, \sigma^2) &= \frac{1}{\sigma\sqrt{2\pi}} exp(-\frac{(x_i - \mu)^2}{2\sigma^2}) \\\ p(X | \mu, \sigma^2) &= (\frac{1}{\sigma\sqrt{2\pi}})^n exp(-\frac{\sum_{i=1}^n(x_i-\mu)^2}{2\sigma^2}) \\\ logp(X| \mu, \sigma^2) &= nlog (\frac{1}{\sigma\sqrt{2\pi}}) - \frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2 \\\ &= - \frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2 + C \end{align}\)

Expanding $logp(\mu|\sigma^2)$ in a similar fashion, eq(18) becomes:

Expanding terms and after completing the square around $\mu$, we find that a Gaussian pops out for $q^*(\mu)$:

Now for $logq^*(\sigma^2)$, expectation $\mathbb{E}$ is evaluated wrt $\mu$, and all terms that do not depend on $\sigma^2$ are collapsed into the constant $C$.

Working from pdf of the inverse-gamma distribution and collapsing terms that don’t depend on $\sigma^2$:

Putting $logq^*(\sigma^2)$ together, we get:

A inverse-gamma pops out for $q^*(\sigma^2)$, where all $\mathbb{E}$ is evaluated wrt $\mu$:

Note the expectation under $q$ for the normal and inverse gamma distributions: \(\begin{align} \mathbb{E}[\mu] &= \mu_n \\\ \mathbb{E}[\sigma^2] &= \frac{\beta_n - 1}{\alpha_n} \end{align}\)

from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
mu, sigma = 0.5, 0.5
data = np.random.normal(mu, sigma, 1000)
plt.hist(data, 30, density=True)


class CAVI():
    def __init__(self, data):
        self.data = data
        self.ndata = len(data)
        self.xbar = np.sum(data)/len(data)
        self.ELBOs = [1, 2]

        # hyperpriors (these don't change)
        self.mu_0 = 0
        self.alpha_0 = 0
        self.beta_0 = 0
        self.sigma_0 = 2
        
        # parameters
        self.mu_n = self.mu_0
        self.alpha_n = self.alpha_0
        self.beta_n = self.beta_0
        self.sigma = self.sigma_0
        self.mu = float(np.random.normal(self.mu_0, self.sigma))
    
    def calc_elbo(self):
        x_mu_sq = np.sum((self.data-self.mu)**2)
        cov_term = -0.5 * (1/self.sigma)
        logp_x = cov_term * x_mu_sq
        logp_mu = cov_term * np.sum((self.data-self.mu_0)**2)
        logp_sigma = (-self.alpha_0 -1) * np.log(sigma) - (self.beta_0/self.sigma)
        
        logq_mu = cov_term*(1/(self.ndata+1)) * ((self.mu-self.mu_n)**2)
        logq_sigma = (self.alpha_n -1)*np.log(self.sigma) - 1/(self.sigma) *(self.beta_n)
        
        ELBO = logp_x + logp_mu + logp_sigma - logq_mu - logq_sigma
        return ELBO
    
    def has_converged(self):
        diff = abs(self.ELBOs[-1] - self.ELBOs[-2])
        return diff<0.01
        
    def coordinate_ascent(self, iterate):
        itr=0
        while itr<iterate and not self.has_converged():
            itr+=1
            self.mu_n = (self.ndata*self.xbar + self.mu_0)/(self.ndata+1) # this actually
converges aft 1 iteration
            self.mu = self.mu_n
            
            self.alpha_n = self.alpha_0 + (self.ndata+1)/2
            self.beta_n = self.beta_0 + 0.5*(np.sum(self.data**2)) - self.xbar*np.sum(self.data) + ((self.ndata+1)/2)*( (self.sigma/self.ndata) + self.xbar**2) - self.mu_0*self.xbar + 0.5*self.mu_0**2           
            self.sigma = (self.beta_n-1)/self.alpha_n
            ELBO = self.calc_elbo()
            self.ELBOs.append(ELBO)
            print("iteration:", itr, "ELBO:", ELBO)

The algorithm converges after 3 iterations in this simple example. We can see coordinate ascent from the following: first the $\mu$ is fitted to the data, followed by $\sigma^2$.

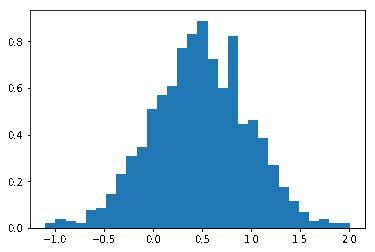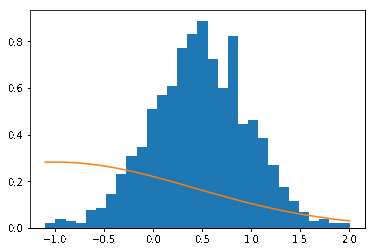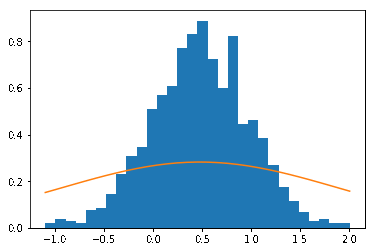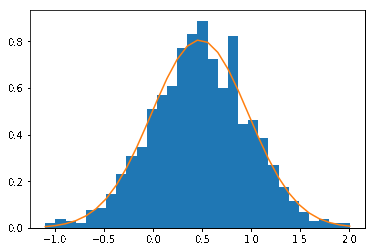
In general Gharamani & Beal showed that if $q$ are from the same exponential family, then we can derive exact updates for the latent variables (which we have done here by brute-force algebra). Also note that because we have estimates of $\mu_n$, $\alpha_n$ and $\beta_n$, we have the entire posterior distribution over the parameters, not just point estimates of $\mu$.

Multivariate Gaussian Mixture Model

1. Specify the generative model: \(\begin{align} x_i &\sim \mathcal{N}(\mu_{z_i}, \Sigma_{z_i}) \\\ z_i &\sim multinomial(\phi_i) \\\ \mu_k &\sim \mathcal{N}(\mu_0, \Sigma_k) \\\ \Sigma_k &\sim \mathcal{W}^{-1}(\Sigma_0, \nu_0) \\\ \phi &\sim Dir(\alpha_0) \end{align}\)

2. The joint distribution where $Z’$ are all latent variables is: \(\begin{align} p(X,Z') &= p(X, Z, \boldsymbol{\phi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) \\\ &= p(X|Z, \boldsymbol{\mu}, \boldsymbol{\Sigma})p(Z|\boldsymbol{\phi})p(\boldsymbol{\phi})p(\boldsymbol{\mu}|\boldsymbol{\Sigma})p(\boldsymbol{\Sigma}) \end{align}\)

3. The variational density is: \(\begin{align} q(Z') &= \prod_{j=1}^m q_j(z_j) \\\ &= q(Z)q(\boldsymbol{\phi})q(\boldsymbol{\mu})q(\boldsymbol{\Sigma}) \end{align}\)

4. ELBO to check convergence. Note the dependence of $\mu$ on $\sigma^2$ under $p$ but their independence under $q$. \(\begin{align} ELBO(q) &= \mathbb{E}[logp(Z, X)] - \mathbb{E}[log q(Z)] \\\ &= \mathbb{E}[logp(X|Z) + logp(Z)] - \mathbb{E}[log q(Z)] \\\ &= \mathbb{E}[logp(X|\mu, \sigma^2) + log p(\mu|\sigma^2) + logp(\sigma^2)] - \mathbb{E}[log q(\mu) + logq(\sigma^2)] \end{align}\)

5. Variational updates

\begin{equation} logq_j(z_j) = \mathbb{E}_{i\neq j}[logp(X, Z’)] + C \end{equation}

For $logq^*(Z)$, expectation $\mathbb{E}$ is taken wrt $\boldsymbol{\phi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}$.

\begin{equation} logq^*(Z) = \mathbb{E}_{\boldsymbol{\phi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}}[logp(X|Z, \boldsymbol{\mu}, \boldsymbol{\Sigma}) + logp(Z|\boldsymbol{\phi})] + C \end{equation}

Recall pdf and logpdf of multivariate normal: \(\begin{align} p(x_i|\mu_k, \Sigma_k) &= 2\pi^{-k/2} det(\Sigma_k)^{-1/2} exp (-\frac{1}{2}(x_i -\mu_k)^T\Sigma_k^{-1}(x-\mu_k)) \\\ logp(x_i | \mu_k, \Sigma_k) &= -\frac{k}{2}log(2\pi) - \frac{1}{2}log det(\Sigma_k) - \frac{1}{2}(x_i -\mu_k)^T\Sigma_k^{-1}(x-\mu_k) \end{align}\)

Absorbing terms that do not depend on $z_{ik}$ into the additive constant:

\begin{equation} log q^*(z_{ik}) = \mathbb{E}_{\boldsymbol{\phi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}}[- \frac{1}{2}log det(\Sigma_k) - \frac{1}{2}(x_i -\mu_k)^T\Sigma_k^{-1}(x-\mu_k) + log(\phi_k)] + C \end{equation}

Since $q(z_i) = \phi_i$ is a distribution over $k$, it needs to be normalised. Therefore the update is: \begin{equation} \phi_{ik} = \frac{exp(logq(z_{ik}))}{\sum_{j}exp(logq(z_{ij}))} \end{equation}

For $q^*(\phi)$, expectation $\mathbb{E}$ is taken wrt $Z, \boldsymbol{\mu}, \boldsymbol{\Sigma}$.

\begin{equation} logq^*(\phi) = \mathbb{E}_{Z, \boldsymbol{\mu}, \boldsymbol{\Sigma}}[log p(Z|\phi) + log p(\phi)] + C \end{equation}

The multinomial $p(z|\phi)$ is: \(\begin{align} p(Z\|\boldsymbol{\phi}) &= \prod_{k=1}^K \prod_{i=1}^n p(z_{ik}\| \phi_k) ^{z_{ik}} \\\ log(p(Z\|\boldsymbol{\phi}) &= \sum_{k=1}^K \sum_{i=1}^n z_{ik} log p(z_{ik}|\phi_k) \end{align}\)

Recall the dirichlet distribution $\phi \sim Dir(\alpha_0)$, where $B$ is a normalizing constant:

Putting things together, and using $\mathbb{E}[z_{ik}] = \phi_{ik}$

which is a dirichlet distribution, $q^*(\boldsymbol{\phi}) = Dir(\boldsymbol{\phi}|\alpha_n)$ with each $k$ component $\alpha_{nk} = \alpha_0 + N_k$

References

Variational Inference: A review for statisticians
Graphical Models and variational methods
[Bishop PRML Approximate Inference (461-473)